CogSci 30PY Project

http://www.comp.leeds.ac.uk/ugadmit/cogsci/tech/hopn.htm:
Hopfield nets can remeber 0.14N states stably, where N is the number of units in the net.

http://www.ida.his.se/ida/kurser/ai_ann/kursmaterial/archive/lectureA.pdf:
Synchronous updates may lead to oscillation and the network may not always converge.
Is this what we need for binocular rivalry?

http://www.nada.kth.se/~asa/hopfield.ps:
for synchronous updating the network may end up flipping between two (but not more) states.

--------------------------------------------------------------------------------------
David J.C. MacKay
Information Theory, Inference, and Learning Algorithms

Ch 32/33 Exact Monte Carlo Sampling / Variational Methods Ch 42 references 33.2, but it is all maths!

Ch 39 The Single Neuron as classifier

Ch 40 Capacity of a Single Neuron

Ch 41 Learning as inference

Ch 42 Hopfield Networks - Explanation starts with Hebbian learning -> Hopfield NNs!

Ch 43 Boltzmann Machines

Hopfield Networks / Boltzmann machines

This book is also available from Amazon

-------------------------------------------------------------------------
C Files for the book  "An Introduction to Neural Networks" by
James A. Anderson,
Department of Cognitive and Linguistic Sciences,
Brown University, Providence, RI 02912., on MIT Press.

-------------------------------------------------------------------------
Hopfield example code from "Neural Networks at Your Fingertips"
--------------------------------------------------------------------------

Background info

Hopfield Networks at Wolfram Research:

Hopfield networks, or associative networks, are typically used for classification. Given a distorted input vector, the Hopfield network associates it with an undistorted pattern stored in the network.

--------------------------------------------------------

NASATech says: The second architecture is that of autoassociative neural networks, which, in nature, enable organisms to recall old memories from partial or noisy stimuli. In an autoassociative network, each neuron is connected to every other neuron in the network. The excitability of any such neuron is determined by the state of all the other neurons and the strengths (weights) of the interconnections between neurons. For any state, the pattern of activation at the next instant in time is completely determined by the preset weights. The number of different firing patterns is 2^n, where n is the number of neurons in the net; because this number is finite, as the sequence of firing patterns proceeds, cycles are inevitable. Cycles that consist of repeated instances of the same pattern are called fixed points, and these fixed points can be chosen by setting the weights to make the points attract nearby patterns. The fixed points represent memories. An autoassociative sensor web could be used to search for known gaseous, biological, or geological signatures, for example.

A chapter on Attractor Networks. This is a good explanation of some of the terms (like "attractor basin").

Oxford Lecture notes on Hopfield Networks and Alzheimer's. Here's a cut from it:

Fusi's PhD thesis, which I've linked to before, seems relevant:
It is about the IT cortex;
context-dependent memory;
recognition but also a no-recognition state (i.e., a spontaneous activity state)
-- p. 6, bottom.

Following are some extracts from his thesis.

From the thesis. Page numbers are from the pdf, not the printed numbers on the page.  (My italics):

Another key property of slow learning is that memory of the class prototypes is always stronger than memory of any other members of the same class which have been shown. This is essential for the classification capability and for reproducing the behavior of the paradigmatic attractor cell. (p. 11)

...the process of learning can be fully described in terms of a few parameters which are the
transition probabilities for LTP and LTD. (p. 11)

...learning requires many presentations of the same stimulus... (p. 11) (over 500)

Stochastic learning provides a good tool for studying quantitatively the process of attractor
formation without specifying the details of the synaptic dynamics. However, to proceed
further, it is important to have a framework that provides a link between the transition
probabilities and the neural activity driven synaptic dynamics. This implies the identification of the source of noise which drives the stochastic mechanism. The solution we propose is suggested by the analysis of cortical recordings: the spike trains recorded in vivo are similar to poissonian processes [Softky Koch 1993] and the variability in the intervals between the spikes of pre- and post-synaptic neurons is a quantity that can be \read" by the synapses. What we show in chapter 7.1 is that it is possible to use this source of
stochasticity to obtain transitions with small probabilities. (p. 13)

Persistent enhanced spike rates have been observed throughout the delay interval between
two successive visual stimulations in several cortical areas: e.g. they are encountered in
infero-temporal (IT) cortex [Fuster, 1990, Fuster & Jervey, 1981, Miyashita & Chang, 1988,
Miyashita, 1988, Sakai & Miyashita, 1991, Miller et al, 1993, Nakamura & Kubota, 1995],
in pre-frontal (PF) cortex [Funahashi et al, 1989, Wilson et al. 1993, Miller et al, 1996,
Scalaidhe et al, 1997, Rao et al. 1997] and in posterior parietal cortex [Koch &Fuster, 1989]
(for a review see [Fuster, 1995]). The phenomenon is detected in single unit extra-cellular
recordings of spikes following, rather than during, the presentation of a sensory stimulus. It
has been found in primates trained to perform a delayed response task, in which the behav-
ing monkey must remember the identity or location of an initial eliciting stimulus in order
to decide upon its behavioral response. The pattern of delay activity is considered a neural
correlate of working memory, which is related to the ability of the animal to actively hold an
item in memory for a short time. In fact, lesions in IT and PF are known to produce impair-
ments in spatial and associative memory tasks [Murrayet al. 1993, Gutnikov et al. 1997],
and a ect recognition of an object after a delay in both humans and monkeys. (p. 15)

The collective aspect is expressed in the mechanism by which a stimulus that had
been learned previously, has left a synaptic engram of potentiated excitatory synapses
connecting the cells driven by the stimulus. When this subset of cells is re-activated by
a sensory event, they cooperate to maintain elevated ring rates in the selective set of
neurons, via the same set of potentiated synapses, after the stimulus is removed. In this
way, these cells can provide each other, i.e. each one of the group, with an a afferent signal
that clearly differentiates the members of the group from other cells in the same cortical
module. (p. 18)

Attractor dynamics (associative memory) implies that each pattern of delay activity is
excited by a whole class of stimuli. Each of these stimuli raises the rates of a sufficient
number of cells belonging to the pattern of activity, so that via the learned collateral
synaptic matrix they can excite the entire subset of neurons characterizing the attractor
and maintain them with elevated rates when the stimulus is removed. (p. 25)

The class of stimuli leading to the same persistent distribution is the basin of attraction of that particular attractor. (pp. 25-26) As one moves in the space of stimuli, at some point the boundary of the basin
of attraction of the attractor is reached. Moving even slightly beyond this boundary,
the network will relax either into another learned attractor, or to the grand attractor of
spontaneous activity. See e.g. [Amit & Brunel, 1997a, Amit, 1995]. (p. 26)

The dynamics of the simplest integrate-and-fire (IF) neuron can be fully described in terms
of a single internal variable: the depolarization V (t) of the neural membrane. The neuron
integrates the afferent current, and when the depolarization crosses a threshold, the neuron
emits a spike. The depolarization is then reset to the hyperpolarization value H, and the
integration process starts again after an absolute refractory period Tarp.
Formally, the differential equation which governs the dynamics below threshold, can be
written as follows:

dV (t) / dt = -L(t1V) + I(t),

where I(t) is the net charging current, expressed in units of potential per unit time, produced by afferent spikes, and L(t) is the leakage term. Usually it is proportional to the depolarization: L(t) = -V(t)/r, where r is the integration time constant of the membrane depolarization. A linear constant decay, not dependent
on V, L(t) = B simplifies the analysis of the collective behavior of the network without sacrificing those features that allow to reproduce the phenomenology of cortical recordings [Fusi & Mattia 1999].
(p. 31. has properly formatted equations)

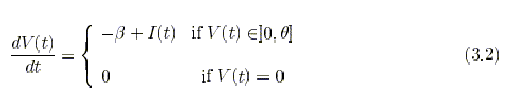(p. 32)

This neuron he calls the LIF neuron (Linear Integrate-and-Fire neuron).3.1.1 The anatomy of the network module

We consider a local module that is a large network containing a number of neurons of
the order of 10^4 - 10^5 . The number of connections between neurons of the same module is
higher than the number of connections between neurons belonging to different modules.
Each neuron is randomly connected to a subset of neurons of the same module through the
recurrent collaterals, and to neurons of other modules through longer range connections
(see Fig.3.1).
In particular, the network module is composed of excitatory (pyramidal) and inhibitory
(inter-neurons) neurons. Each neuron has some probability (connectivity level) of a
synaptic contact with any other neuron (excitatory or inhibitory) of the same module, and
receives external excitatory afferents from pyramidal neurons of other modules.
The connectivity structure can be fully described in terms of two sets of variables:
the binary variables cij of having a connection between neuron j (pre-synaptic neurons)
and neuron j (post-synaptic neuron) and the corresponding synaptic weight Jij . In what
follows the cij are generated at random and never changed, while the synaptic couplings
Jij can vary to acquire information about the stimuli that excite part of the neurons of the
network module. (p. 32)

SD = signal dominated (p. 33)
ND = noise dominated (p. 34)

Each neuron will receive a current Ii(t) (i denotes the index of the neuron) given by:

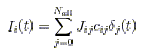(p. 32)

where cij is 1 if there exists a synaptic contact between neuron j and neuron i, Jij is
the corresponding synaptic strength, and the sum extends over all the Nall neurons of the
populations (recurrent or external) that are interacting.

"Such being the nature of our subject and such our way of arguing in our discussion of it, we must be satisfied with a rough outline of the truth."

-Aristotle

Binocular Rivalry

Cognitive Science

Home