| Anvendt geometri |  |
| "Av alt vås er vitenskapens det verste, | |
| fordi det er så fordømt logisk og gjennomtenkt." | |
| -Louis-Ferdinand Céline i 'Reisen til nattens ende'. |
1. Vektorer
Begrepet vektor innen matematikken må ikke forveksles med vektor-begrepet innen programmering. (I Java, for eksempel, er Vector en standardklasse for å lagre et arbitrært antall objekter.)En vektor er et linjesegment som har retning. En vektor blir karakterisert ved sin lengde og ved sin retning.
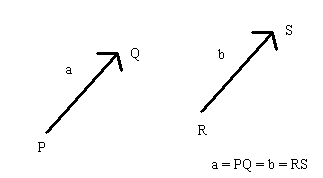
Summen av to vektorer a og b skrives
c = a + b
og er diagonalen av et parallelogram, der a, b og c starter i samme punkt.
Lengden av en vektor a skrives |a|. En vektor med null i lengde blir kaldt null-vektoren, skrevet 0. Notasjonen -a blir brukt for vektoren som har lengden |a| og som har motsatt retning av a.
For enhver vektor a og et reelt tall c, har vektoren ca lengden c|a|. Hvis a = 0 eller c = 0, så er ca = 0. Ellers har ca retingen a hvis c > 0 og motsatt retning hvis c < 0.
Følgende gjelder for vektorene u, v, w og de reelle tallene c og k.
u + v = v + u
(u + v) + w = u + (v + w)
u + 0 = u
u+ (-u) = 0
c(u + v) = cu + cv
(c+k)u = cu + ku
c(ku)
2. Det indre produkt
3. Determinanter
4. Vektorprodukt
5a. Tre punkters retning (orientation)
5b. En alternativ, to-dimensjonal løsning
6. Polygoner
7. Arealet av en ploygon
8. Punkt-i-triangel testen
9. Punkt-i-polygon testen
10. Punkt-på-linje testen
11. Avstanden mellom et punkt og en linje
12. Projeksjonen av et punkt på en linje
13. Triangulering av polygoner
