Part 3: Logic
Sources: Hurley, Penny Rush lecture series at La Trobe University, spring 2001, My Norwegian pages on logic, The Discrete Maths pages on logic.
3.1 Basic concepts
3.1.1 Arguments
A group of statements in which one or more of the statements (the premises) are claimed to provide support for, or reasons to believe, one of the others (the conclusion).
An argument has a factual claim and an inferential claim.
3.1.2 Statements
See The Discrete Maths page on logic.
3.1.3 Premises
The statement(s) which are supposed to provide evidence for the conclusion.
3.1.4 Conclusion
What is trying to be shown.
3.1.5 Non-arguments
3.1.5.1 Illustrations
An illustration (an instance of something, to provide an example), is not an argument per se, but you can have an argument from example. If a statement is not easily believed, then a (number of) example(s) may try to persuade you into believing the statement.
3.1.5.2 Explanations
An explanation does not try to argue something, but simply to shed light on something. An explanation consists of an explandandum (what is to be explained) and an explanans (the part that explains).
3.1.6 Deduction and induction
3.1.6.1 Deductive arguments
In a deductive argument, it is impossible for the premises to be true and the conclusion to be false (see truth-table for implication). A deductive argument usually (but not always) argues from "the general" to "the particular".
For example:
P1. All hackers are people who know computers.
P2. All people who know computers are born after 1840.
C. All hackers are born after 1840.
If the two premises are true, then it is impossible for the conclusion to be false.
You see that in a deductive argument, all the information in the conclusion is contained in the premises.
3.1.6.1.1 Types of deductive arguments
1 .An argument based on mathematics (except statistic arguments, which
are usually inductive).
2. An argument from definition.
3. A categorical syllogism.
4. A hypothetical syllogism.
5. A disjunctive syllogism.
3.1.6.1.2 Validity
A valid deductive argument is an argument of a form in which it is actually impossible for the premises to be true and the conclusion to be false. If an argument has the form of a deductive argument, but it is still possible to have false premises and a true conclusion, the argument is invalid. Hence, the argument
P1. All trees are blue.
P2. The plant outside my window is a tree.
C. The plant outside my window is blue.
is a valid argument, even though the premises are not true. This is because; if the premises had been true, it would force the conclusion to be true. If all trees are blue, then the tree outside my window would be blue also.
On the other hand, the argument
P1. My mother can swim.
P2. Swans can swim.
C. My mother is a swan
is invalid, because it is possible for the premises to be true, and the conclusion to be false.
Soundness
A sound argument is a valid argument with true premises.
3.1.6.2 Inductive arguments
In an inductive argument, it is improbable for the premises to be true and the conclusion to be false. An inductive argument usually (but not always) argues from "the particular" to "the general".
For example:
P1. The vast majority of hackers eat a lot of pizza.
P2. Otto is a hacker.
C. Otto eats a lot of pizza.
If the two premises are true, then it is probable that the conclusion is true. But it might not be.
This is an example of an inductive argument that proceeds from the general to the particular (which is not the way an inductive argument usually proceeds):
P. Every day so far the sun has risen.
C. Therefore, the sun will rise tomorrow.
Given that the premise is true (and it is), then it is highly probable that the conclusion is true. But it might not be. The sun might go extinct, or a huge meteor may crash into the sun and push it away from the Earth. Hence, it is an inductive argument.
3.1.6.2.1 Types of inductive arguments
1. An inductive generalisation.
2. An argument from authority.
3. An argument based on signs.
4. A causal inference.
3.1.6.2.2 Strong and weak inductive arguments
A strong inductive argument is an argument where it is probable that the conclusion is true if the premises are true. A weak inductive argument is an argument where it is not probable that the conclusion is true if the premises are true, even though the argument claims so.
E.g., a strong inductive argument:
P1. All men seen so far have been immortal.
P2. Sten Andersen is a man.
C. Sten Andersen is mortal.
The premises are true, so the conclusion is highly probable. (It might be argued that being mortal is actually part of being a man, in which case the argument would not be inductive. If we one day where confronted with an immortal man, we would then have to say he was actually no man at all, but some other kind of being. But if we accept that an immortal man is still a man [even though we would not expect to meet one], the argument, as it appears above, is inductive.)
Another strong argument:
P1. All men seen so far have pink tails.
P2. Sten Andersen is a man.
C. Sten Andersen has a pink tail.
Even though on of the premises is false, this argument is still strong, because if both premises had been true, then the conclusion would probably follow. But the argument
P1. Some children have been born with two hearts.
P2. Chris is a child.
C. Chris has been born with two hearts.
is a weak one, because the conclusion does not follow with a high probability from the premises.
Cogency
If an inductive argument is strong and the premises are true, then the argument is cogent.
3.2 Argument forms
The form of an argument is the way the argument is built. Through inspecting the form alone, we can se if the argument is valid or not. But to check if the argument is sound or not, we have to go into "the real world" and find out if the premises are actually true.
An argument of the form
P1. All A are B
P2. All B are C
C. All A are C
is valid. Any term could be substituted for A, B, and C, and the argument would still be valid.
But the argument
P1. All A are B
P2. All C are B
C. All A are B
is on an invalid form.
The last couple of arguments have been what are called categorical syllogisms. The next example is a hypothetical syllogism:
P1. If p, then q
P2. p
C. q
of the valid form modus ponens (here is an explanation of modus ponens in Norwegian). For a discussion of implication, see The Discrete Maths page on logic (or: implikasjon, Norwegian).
However, an argument of the form
P1. If p, then q
P2. q
C. p
is not valid.
Again, if the argument is on a valid form, we can check if it is sound by going into "the real world" and checking if the premises are true. Only if the argument is valid and the premises are true, is the argument sound.
To prove that an argument form is invalid, we may try to find an argument on that form where the premises are true and where the conclusion is false, e.g.,
P1. Some animals are not mammals.
P2. All cats are animals.
C. Therefore, all cats are not mammals.
3.3 Categorical syllogisms
A syllogism is an argument with two premises and one conclusion.
A proposition is a sentence which is either true or false. A categorical proposition claims that all or part of the class picked out by the subject terms, is included or excluded from the predicate term.
We will introduce a shorthand notation for the four different kinds of categorical propositions.
| Quantifier | Subject | Copula | Predicate | Quality | Quantity | Shorthand |
| All | S | are | P | pos | universal | A |
| No | S | are | P | neg | universal | E |
| Some | S | are | P | pos | particular | I |
| Some | S | are not | P | neg | particular | O |
Thus, SaP means All S are P, BeI means No B are I, and so on. If a categorical proposition is in one the above forms, it is in standard form.
A syllogism is an argument with two premises and one conclusion; a categorical syllogism is an argument about categories, the argument having (yes, you guessed it), two premises and one conclusion. We have seen such arguments before, for example
P1. All M are P (MaP)
P2. All S are M (SaM)
C. All S are P (SaP)
(S = subject, M = middle term, P = predicate)
All premises in this argument are of the A- type, this is called the AAA form. There are four ways to distribute the subject, middle term, and predicate:
| 1 | 2 | 3 | 4 | |
| P1 | M P | P M | M P | P M |
| P2 | S M | S M | M S | M S |
| C | S P | S P | S P | S P |
Hence, the former argument is called an AAA-1 syllogism (this valid syllogism actually has a name, it is called Barbara).
The Ms in this table have been highlighted only to give you a way of remembering the table. Notice that the Ms in 2 and 3 are hugging, that the 1st premise always contains the predicate and the 2nd always the subject, and that the conclusion is always on the form subject - predicate.
The subject is called the minor term, the predicate is called the major term. Don't worry, it will be repeated.
Even though you might not feel ready for it yet, I'm going to present you with a table of valid syllogistic forms. It is going to be handy later, when we are to judge whether a categorical syllogism is valid or not (duh).
Unconditionally valid
| 1 | 2 | 3 | 4 |
| AAA | EAE | IAI | AEE |
| EAE | AEE | AII | IAI |
| AII | EIO | OAO | EIO |
| EIO | AOO | EIO |
Conditionally valid
| 1 | 2 | 3 | 4 | Required condition |
| AAI | AEO | AEO | S exist | |
| EAO | EAO | " | ||
| AAI | EAO | M exist | ||
| EAO | " | |||
| AAI | P exist |
5 rules for categorical syllogisms (stolen almost directly from Hurley)
1. The middle term must be distributed at least once.
Fallacy: Undistributed middle.
2. If a term is distributed in the conclusion, then it must be distributed
in the premise.
Fallacy: Illicit major; illicit minor.
3. Two negative premises are not allowed.
Fallacy: Exclusive premises.
4. A negative premise requires a negative conclusion, and a negative
conclusion requires a negative premise.
Fallacy: Drawing an affirmative conclusion from a negative premise; drawing
a negative conclusion from affirmative premises.
5. If both premises are universal, the conclusion cannot be particular.
Fallacy: The existential fallacy. If this rule is broken, the syllogism
is conditionally valid; i.e., valid on condition that certain terms denote
actually existing things.
3.3.1 Venn diagrams
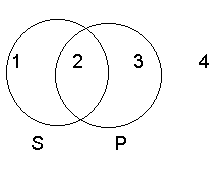
3.4 Fallacies
3.4.1 Informal fallacies
An informal fallacy is a fallacy that can only be found by inspecting the content of an argument. This is in contrast to a formal fallacy, which may be found by looking at the form of the argument.
A fallacy may be committed if the same word is used with two different meanings in one argument. Hurley gives the following example:
P1. All factories are plants.
P2. All plants contain chlorophyll.
C. All factories contain chlorophyll.
It may look like this is an argument on the form AAA-4, which is unconditionally valid. But, inspecting the argument, you find that the word "plant" has two different meanings, hence the argument really goes
P1. All A are B
P2. All C are D
C. All A are D
which, of course, is pure rubbish.
3.4.1.1 Fallacies of relevance
Appeal to force (Argumentum ad Baculum)
Appeal to pity (Argumentum ad Misericordiam)
Appeal to the people (Argumentum ad Populum)
Direct / indirect. Bandwagon, appeal to vanity, appeal to snobbery.
Argument against the person (Argumentum ad Hominem)
abusive, circumstantial, tu quoque
Accident
Straw man
Missing the point (Ignoratio Elenchi)
Red herring
3.4.1.2 Fallacies of weak induction
Appeal to unqualified authority (Argumentum ad Verecundiam)
Appeal to ignorance (Argumentum ad Ignoratium)
Hasty generalisation (Converse accident)
False cause
Slippery slope
Weak analogy
3.4.1.3 Fallacies of presumption, ambiguity, and grammatical analogy
3.4.2 Formal fallacies
![]()